Part I – Dissimilarity Index
White compared to Black:
∑ |a-b|
= 90.56
DI = 45.28 – meaning 45.28% of black people
would have to move in order to have an equal distribution of white people and
black people.
White
compared to Asian:
∑ |a-b|
= 78.93
DI = 39.46 – meaning 39.46% of Asians would
have to move in order to have an equal distribution of white people and Asians.
White
compared to Hispanic:
∑ |a-b|
= 77.45
DI = 38.73 – meaning 45.28% of Hispanics
would have to move in order to have an equal distribution of white people and
Hispanics.
These
results show that around 40% of the population would have to move in order to
have an even distribution of the races in each census tract. The maps show that
Non-Whites are by far concentrated in the central parts of Madison and Dane
County. Non-whites would have to move out into the suburbs of Madison and the
surround small towns in Dane County in order to have an equal distribution of
Whites and Non-whites.
Part II – Kitchen Sink
Hypotheses
The
Null Hypothesis is that there is no linear relationship between Number of
Foreclosures per 100 persons and High Cost Loans. The Alternative Hypothesis is
that there is a linear relationship between Number of Foreclosures per 100
persons and High Cost Loans.
The
Null Hypothesis is that there is no linear relationship between Number of
Foreclosures per 100 persons and Percent of people with Mortgages. The
Alternative Hypothesis is that there is a linear relationship between Number of
Foreclosures per 100 persons and Percent of people with Mortgages.
The
Null Hypothesis is that there is no linear relationship between Number of
Foreclosures per 100 persons and Percent of Black people. The Alternative
Hypothesis is that there is a linear relationship between Number of
Foreclosures per 100 persons and Percent of Black people.
The
Null Hypothesis is that there is no linear relationship between Number of
Foreclosures per 100 persons and Percent of White people. The Alternative
Hypothesis is that there is a linear relationship between Number of
Foreclosures per 100 persons and Percent of White people.
The
Null Hypothesis is that there is no linear relationship between Number of
Foreclosures per 100 persons and Percent of Non-white people. The Alternative
Hypothesis is that there is a linear relationship between Number of Foreclosures
per 100 persons and Percent of Non-white people.
The
Null Hypothesis is that there is no linear relationship between Number of
Foreclosures per 100 persons and Percent of Asian people. The Alternative
Hypothesis is that there is a linear relationship between Number of
Foreclosures per 100 persons and Percent of Asian people.
The
Null Hypothesis is that there is no linear relationship between Number of
Foreclosures per 100 persons and Unemployment. The Alternative Hypothesis is
that there is a linear relationship between Number of Foreclosures per 100
persons and Unemployment.
The
Null Hypothesis is that there is no linear relationship between Number of
Foreclosures per 100 persons and Commuting Minutes. The Alternative Hypothesis
is that there is a linear relationship between Number of Foreclosures per 100
persons and Commuting Minutes.
The
most significant variables were HighCostLoans and PerMortgage10. I know this
because of their low significance values which were close to 0; no other
variables had significance values under the required 0.05. They also had
positive betas which show that they increase as the dependent variable
increase.
At
first there was some multicollinearity because of the variable PerBlack. I knew
this because of the Eigen value that were close to zero and the condition
indexes that were over 30. Once I had removed this variable the
multicollinearity disappeared.
PerNonwhite
was exclude right away meaning that the variable was just so far from
significant the regression didn’t include it. I then removed the remaining
variables that were not found significant which included PerWhite, ComMins10 and
Unemploy10, PerAsian. I had to rerun the statistics five times in order to get
my final equation by removing the least significant variable each time until
there were only significant variables left.
At
first the significance value was 0.090 for PerMortgage10 but by the time that I
had eliminated all other variables beside PerMortgage10 and HighCostLoans the
significance value had gone down to 0.017 which is below the 0.05 needed to be
significant.
For
Number of Foreclosures per 100 persons and High Cost Loans I reject the null
hypothesis. There is a linear relationship between the two.
For
Number of Foreclosures per 100 persons and Percentage of people with mortgages I
reject the null hypothesis. There is a linear relationship between the two.
For
Number of Foreclosures per 100 persons and Percent of Black people I fail to
reject the null hypothesis. There is no linear relationship between the two.
For
Number of Foreclosures per 100 persons and Percent of White people I fail to
reject the null hypothesis. There is no linear relationship between the two.
For
Number of Foreclosures per 100 persons and Percent of Non-white people I fail
to reject the null hypothesis. There is no linear relationship between the two.
For
Number of Foreclosures per 100 persons and Percent of Asian people I fail to
reject the null hypothesis. There is no linear relationship between the two.
For
Number of Foreclosures per 100 persons and Unemployment I fail to reject the
null hypothesis. There is no linear relationship between the two.
For
Number of Foreclosures per 100 persons and Commuting Minutes I fail to reject
the null hypothesis. There is no linear relationship between the two.
My
final equation is y = -0.10 + 0.004x1
+ 0.004x2
The variables
are
y = Number
of Foreclosures per 100 persons (Count2011)
x1
= High Cost Loans (HighCostLoans)
x2
= Percent of people with mortgages (PerMortgage10)
My
results show that high cost loans and percent of people with mortgages have
significant correlations with the number of foreclosures per 100 persons. I can
use this equation to predict the number of foreclosures per 100 persons in a
given census tract if I have the data for high cost loans and percent of people
with mortgages.
Part III – Stepwise
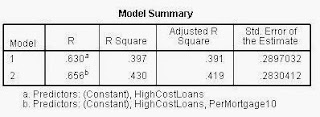
 |
| SPSS results from a Stepwise Regression. |
I ended
up with the same model as the Kitchen Sink Approach:
Final
equation is y = -0.10 + 0.004x1
+ 0.004x2
The variables
are
y = Number
of Foreclosures per 100 persons (Count2011)
x1
= High Cost Loans (HighCostLoans)
x2
= Percent of people with mortgages (PerMortgage10)
The
Stepwise Regression gives me the same model and equation as the Kitchen Sink
Approach, however it does it in one step instead of multiple. That’s awesome
that the stepwise approach can do all of that analysis by itself; it saves time
in having to rerun the regression over and over until I get an equation.
Prediction:
x1
= 80.0 High Cost Loans
x2
= 50.0% Drive to Work
y = -0.10 + 0.004(80.0) + 0.004(50.0)
y = -0.10 + 0.32 + 0.20
y = 0.42
According
to my model, having 80 high cost loans and 50% of people driving to work in a
given census tract you will get 0.42 foreclosures per 100 persons in that
census tract.
I am somewhat
confident in my results due to the okay R2 value of 0.430 that I had
in my model. The high significance that the two variables I used helps the confidence
that I have in the model, but the R2 value is the most important
sign of the strength of a model. So, I would say that my model is moderately adequate.



No comments:
Post a Comment